Newton for Flerfs (Part 1)
As mentioned in a previous post I get trapped by Facebook reading flerf/anti-flerf posts. However, I like to come at the discussion from a mathematical point of view.
A common flerf post is that if the earth is really spinning at 1000 miles per hour why are we not thrown off the side if it. This is often accompanied by pictures of kids roundabouts or fair ground rides, with people enjoying the g-force generated from these.
As fortune would have it calculating how much g-force you will experience on a spinning object has been covered by science (hundreds of years ago). Even better it can be entirely derived from first principals (you will need to read a book on calculus to see this done).
Anyway, I thought that it would be interesting to calculate just how much outward force the earth is putting on us at the equator assuming that it is indeed round and has the circumference scientists claim.
The claim is that we are moving round a circle at a constant rate. So we want a set of equations that constantly move us around a circle as time moves on:
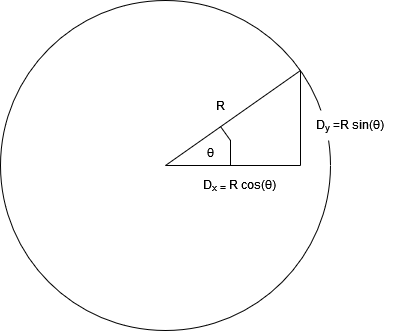
Using these two equations as \(\theta\) moves from \(0-360^{\circ}\) the location will move around the circle. We want to complete 1 rotation every \(T_r\) seconds giving the equations:
\[ D_x = R \cdot cos(\frac{360 \cdot t}{T_r}) \] \[ D_y = R \cdot sin(\frac{360 \cdot t}{T_r}) \]
Now as \(t\) (our variable) moves from \(0-T_r\) seconds we will trace a path around the circle. We need to make one final adjustment to the equation and that is to use radians instead of degrees. With radians circles are split into \(2\cdot \pi\) sections instead of \(360^{\circ}\). \(sin\) and \(cos\) are actually calculated using radians, your calculator scales degrees to radians before calculating them. Using radians from the start makes the mathematics simpler (all reasonable calculators will have a mode to use radians instead of degrees):
\[ D_x = R \cdot cos(\frac{2 \cdot \pi \cdot t}{T_r}) \] \[ D_y = R \cdot sin(\frac{2 \cdot \pi \cdot t}{T_r}) \]
- \(D_x\) is our horizontal distance from the center
- \(D_y\) is our vertical distance from the center
- \(R\) is the radius of our circle
- \(t\) is our current time in seconds
- \(T_r\) is the time for one complete rotation in seconds
Now given distance equations we can use a mathematical tool called differentiation to calculate velocity equations:
\[ V_x = \frac{-2\cdot R\cdot \pi}{T_r} \cdot sin(\frac{2 \cdot \pi \cdot t}{T_r}) \] \[ V_y = \frac{2\cdot R\cdot \pi}{T_r} \cdot cos(\frac{2 \cdot \pi \cdot t}{T_r}) \]
Now this gives us components of a velocity. We can use Pythagoras on this to work out the speed instead:
\[Speed = \frac{2 \cdot R \cdot \pi}{T_r}\]
Because of the trig identity \(cos^2(\theta) \times sin^2(\theta) = 1\) when we do the Pythagoras we lose our trig terms, and our dependence on \(t\). This is good as it proves that the distance equation moves us round the circle at a constant speed (like on a roundabout, which is what we wanted).
Now we have a the velocity components we can use differentiation again to work our our acceleration:
\[ A_x = \frac{-4\cdot R\cdot \pi^2}{T_r^2} \cdot cos(\frac{2 \cdot \pi \cdot t}{T_r}) \] \[ A_y = \frac{-4\cdot R\cdot \pi^2}{T_r^2} \cdot sin(\frac{2 \cdot \pi \cdot t}{T_r}) \]
Again these equations contain direction information as well as the magnitude of the acceleration. To work out the magnitude of the acceleration we can again use Pythagoras to give:
\[Acceleration = \frac{4\cdot R\cdot \pi^2}{T_r^2}\]
As we now have a equation for speed and acceleration we can now plug some values in to work out how much acceleration/force you would feel in different situations. So on a roundabout which is 2 meters wide and spinning once a second:
- \(R = 1\) (a 2 meter diameter gives a 1 meter radius).
- \(T_r = 1\)
Then:
- \(Speed = 6.28 m/s\)
- \(Acceleration = 39.47m/s^2\)
Now if we imagine a fair ground ride with a 5 meter radius, which takes 5 seconds to complete a rotation then:
- \(Speed = 6.28 m/s\)
- \(Acceleration = 2.5m/s^2\)
This is why these rides feel quite gentle, we’re going at the same speed as we do on a roundabout, except round a much bigger circle so the acceleration required to keep us on that circle is considerably less. It’s also why roundabouts are so fun.
Finally, the values for the planet we live on, at the equator:
- \(R = 6,378,137m\)
- \(T_r = 86,400s\) - number of seconds in a day (to complete 1 rotation)
Then:
- \(Speed = 46,400 m/s = 1,670kph = 1,038mph\)
- \(Acceleration = 0.03m/s^2\)
At this acceleration at the equator it would take more than 13 minutes to go from 0 to 60mph, a barely noticeable acceleration, even slower than my Toyota Aygo. And fortunately gravity is pulling with a much large acceleration than that, keeping you stuck firmly to the ground. In fact, if gravity was 300 times weaker as a force there would still not be enough force from the spin of the earth to send anything flying off of it.
Note that the equations in this are fundamental mathematics and can be derived from first principals. They are in-arguably true and you can either do a course in mathematics or read a book to find the logical proofs of these. The physical quantities are made up (or looked up in the case of the earth), I haven’t measured a fair ground ride or a roundabout, or the number of seconds it takes them to spin. Feel free to do so and put the results into the equations if you like. If you’ve got young kids you can add a bit of science to their play activity!